If you’re interested in using GMac you probably already know about Geometric Algebra. Before using GMac, or any other GA-based software, a firm mathematical GA background is needed. Eric Chisolm’s paper is a very good introduction to start with. A more detailed view of the subject can be found in these books:

• The simplest book to start with is “Understanding Geometric Algebra: Hamilton, Grassmann, and Clifford for Computer Vision and Graphics” by Kenichi Kanatani. (online). This book is excellent for teaching a simple GA yet powerful introduction to undergraduates in various fields.
• An essential book for computer scientists, especially in computer graphics, is “Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry” by Leo Dorst, Daniel Fontijne, and Stephen Mann (online, and book website). This book is an essential reference for any serious study of GA for practical purposes including software implementations for geometric algebra algorithms.
• Many good basic GA ideas, both algebraic and geometric, can be found in “Geometric Algebra with Applications in Engineering” by Christian Perwass (online). The book contains many interesting applications in engineering to illustrate the powerful modeling capabilities of geometric algebra.
• The book “Foundations of Geometric Algebra Computing” by Dr. Dietmar Hildenbrand contains a good introduction to geometric algebra with emphasis on Conformal Geometric Algebra (online). The book also has a nice collection of practical applications using various tools like Maple for symbolic GA computing, CLUCalc for numerical GA computations and visualizations, Gaigen for optimizing runtime performance of GA computations, Gaalop and the Gaalop Precompiler tools for high-performance GA computing, and illustrations of parallel hardware implementations of GA algorithms.

More GA resources can be found in the GA Online Resources page. I’ve written my own GA introduction specific to the way I thought while creating GMac. This guide is not intended to explain GA but rather to point out the basic mathematical constructions using which GMac is implemented as a software system. In other words, the focus is on the GA math-related software infrastructure of GMac, not on the GA math itself.

GMac deals with Geometric Algebra mathematical constructions like frames, multivectors, and outermorphisms. To symbolically represent and manipulate these mathematical constructs in software, we need to use a significant amount of organized symbolic processing that can only be provided practically by a Computer Algebra System (CAS). If you read the GMac System Guide, you find that symbolic processing is a core component of GMac. Currently, the computer algebra system GMac depends on is Wolfram Mathematica.

Inside the GMac system, there is a namespace called SymbolicInterface that contains the necessary code for interfacing with Mathematica from .NET in a well managed OOP way. In addition, the namespace called GMac.GMacCompiler.Symbolic extends the SymbolicInterface classes to implement symbolic processing of GA frames, multivectors, and outermorphisms. In addition, the GMac.GMacUtils namespace contains some static utility classes for implementing basic mathematical computations needed for GMac to represent and manipulate GA basis blades using bitwise operations on integers, among other fundamental functions. This guide will explain the connections between the classes under these namespaces to GA computations. The classes under these namespaces can be used for any other project as a symbolic implementation of GA computations. You can use GMac itself to generate a solid numeric implementation for any desired GA space as explained in the other GMac Guides.

---

1. The General Symbolic Interface

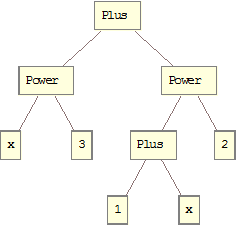Most computer algebra systems deal explicitly with a single type of data: the expression tree. For example, in Mathematica the expression x^3 + (1 + x) ^2  is internally represented as the shown tree. The system operates by manipulating such expression trees, following mathematical logic laws, to create other meaningful symbolic trees. For example, the system can substitute the number 9 for the symbol x in the tree and evaluate the whole expression using some sort of tree-visitor algorithm to obtain the value 829 for the whole expression. Many symbolic algebraic manipulations can be done using this simple technique. To enable the system to handle new algebraic constructs not already defined, like geometric algebra, you need to define two things:

• The general structure of expression trees representing the main mathematical structures of the new algebra.
• The rules of manipulating the tree structures that correspond to the actual mathematical rules of the algebra.

We can also define new algebraic rules from old ones. For example, we can define a symbolic structure for complex numbers, say Complex[r, m], taking two real numbers, and then define the addition, product, division, and all other complex algebra operations using operations in real numbers.

The main problem with this approach is its conceptual distance from Object Oriented Programming (OOP) used in systems like GMac. I had to create a layer of classes that stores internally Mathematica’s expression trees, while providing an OOP interface for GMac. The SymbolicInterface project contains the main classes for this particular purpose. My intent is to gradually create a unified interface for systems like GMac to communicate with several CAS like Mathematica, Maple, SageMath, SymPy, etc.

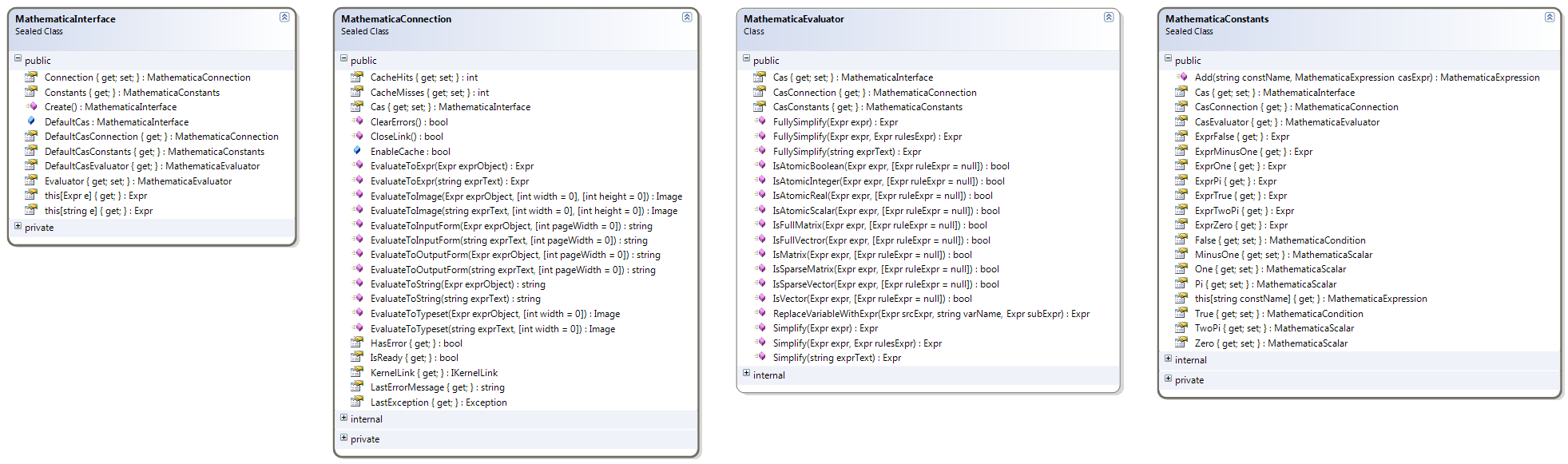
1.1. The Mathematica Interface Classes

Under the SymbolicInterface.Mathematica namespace we find 4 classes serving the purpose of the OOP interface with Mathematica:

1. The MathematicaInterface class is our starting point. This class contains automatically created instances of the other 3 classes. It can also be used to convert Mathematica’s Expr objects to and from their textual representations.
2. The MathematicaConnection class is responsible for creating, closing, using, and maintaining the . NET/Link API object of type IKernelLink that performs the Mathematica-.NET communications. This class can be used to create and close an instance of the Mathematica kernel in the background, and to evaluate and convert Mathematica expressions, both in text and treelike  Expr forms, into other expressions, strings, or images.
3. The MathematicaConstants class contains a list of useful constants used in symbolic computations like Pi, e, Zero, etc.
4. The MathematicaEvaluator class contains some commonly used methods for evaluating and simplifying symbolic expressions in their text or Expr tree forms.

The exact members and methods of these classes will be frequently updated as the future needs dictate.

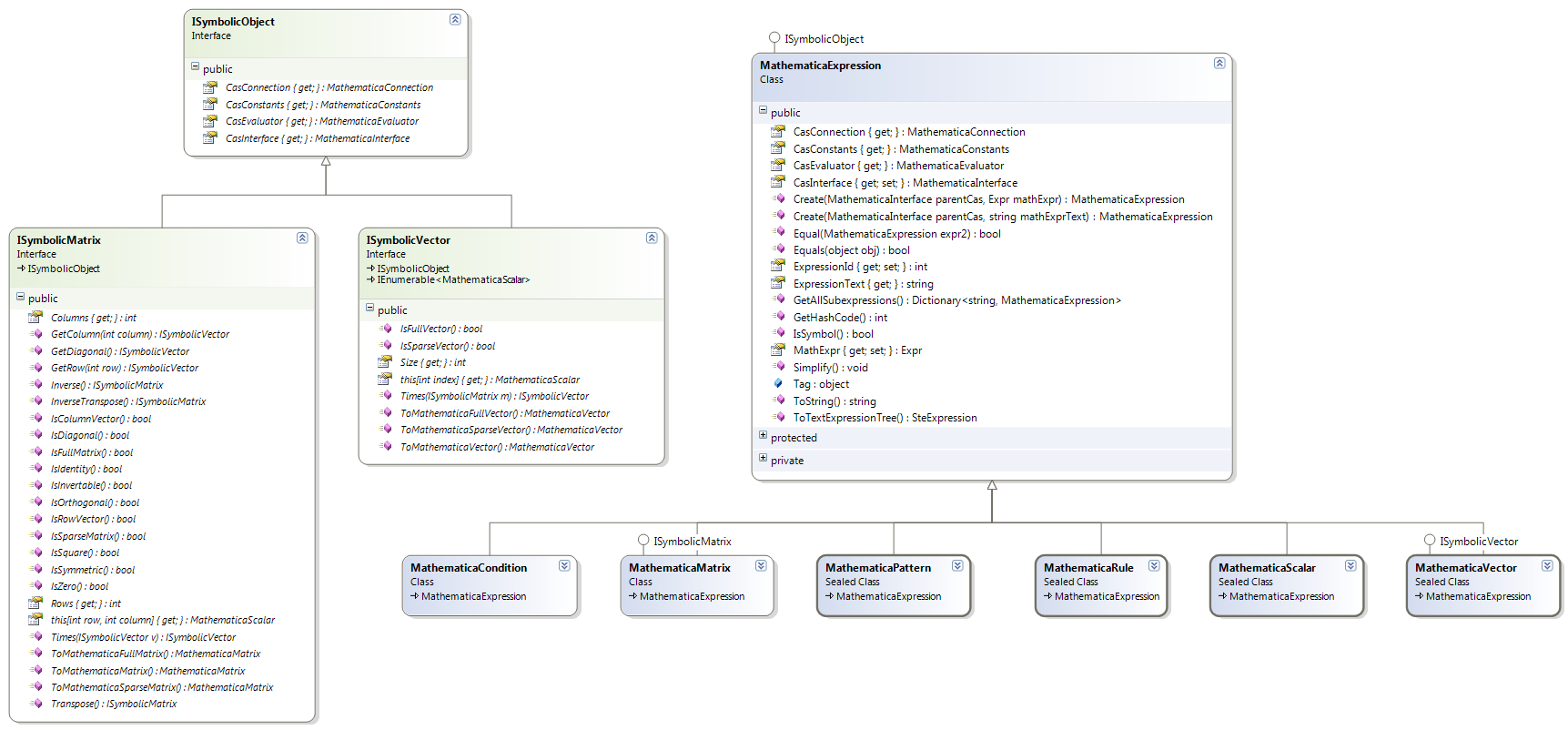
1.2. The Mathematica Expression Classes

Since everything in Mathematica is an expression, we can’t depend on the Expr class to distinguish operations logically applicable to one type of expression or the other. For example, Expr objects can represent:

• All kinds of numbers: integers, rationals, reals, and complex numbers.
• Lists of anything: real vectors, 1-column\1-row complex matrices, lists of symbols, etc.
• Arrays of anything.
• Sparse lists and sparse arrays.
• Discrete mathematics’ structures; like trees and graphs.
• Images of many kinds.
• Mathematical functions: like sin, tan, square root, etc..
• Abstract algebraic structures: like rings, groups, and finite fields.
• Boolean conditions and comparisons used as constraints in equations and algorithms like x > 6 and 3 y = 2 z.
• And much more.

Naturally, each of these conceptually different entities has its own set of operations and relations with other entities not captured in the Expr object at compile time; only at run time depending on the exact tree structure in the Expr object. The solution to this problem, a serious one in OOP systems, is to create a wrapper class hierarchy around the Expr objects to capture the differences at compile time. The base class of the wrapper hierarchy is the MathematicaExpression class under the SymbolicInterface.Mathematica.Expression namespace.

 

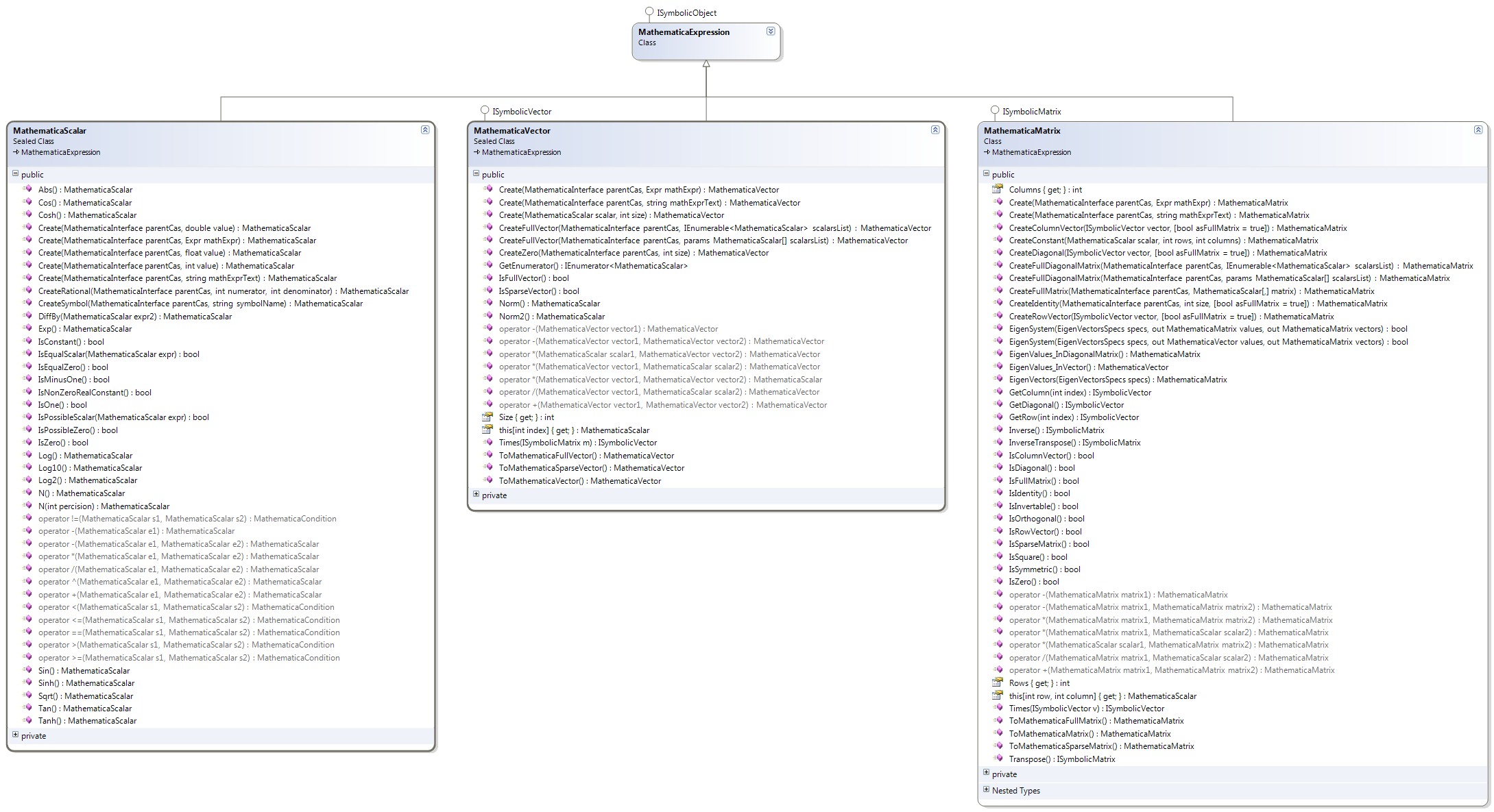
The MathematicaExpression class can be used by itself to hold and simplify any arbitrary Mathematica Expr tree object. Several classes inherit from this class to represent different kinds of common symbolic expressions like real scalars, real vectors, and real matrices along with properties and methods appropriate to each. The MathematicaScalar class, for example, is used extensively inside GMac code for manipulating scalar coefficients of multivectors and other GA-related constructs.

 1.3. Expression Construction Helper Classes

Under the SymbolicInterface.Mathematica.ExprFactory namespace we find several classes for creating Expr object trees in an OOP manner:

• The DomainSymbols static class contains Expr objects representing mathematical domains like real numbers, rational numbers, complex numbers, etc.
• The CharacterSymbols class can be used to create expressions representing notational alphabetic characters like Script, Gothic, Formal, and Double Struck symbolic characters.
• The Mfs class can be used to construct common Mathematica functions with Expr arguments. For example, this C# code will create the expression tree corresponding to the mathematical expression   x^3 + (1 + x)^2  : Mfs.Plus[Mfs.Power["x".ToSymbolExpr(), 3], Mfs.Power[Mfs.Plus[1, "x".ToSymbolExpr()], 2]] . This method is useful for creating complicated Expr objects from a run-time data source; we could have used the MathematicaInterface indexer property to directly parse the string   "x^3 + (1 + x)^2" into an Expr object, which is more suitable for this particular example.

---

2. The Geometric Algebra Symbolic Interface

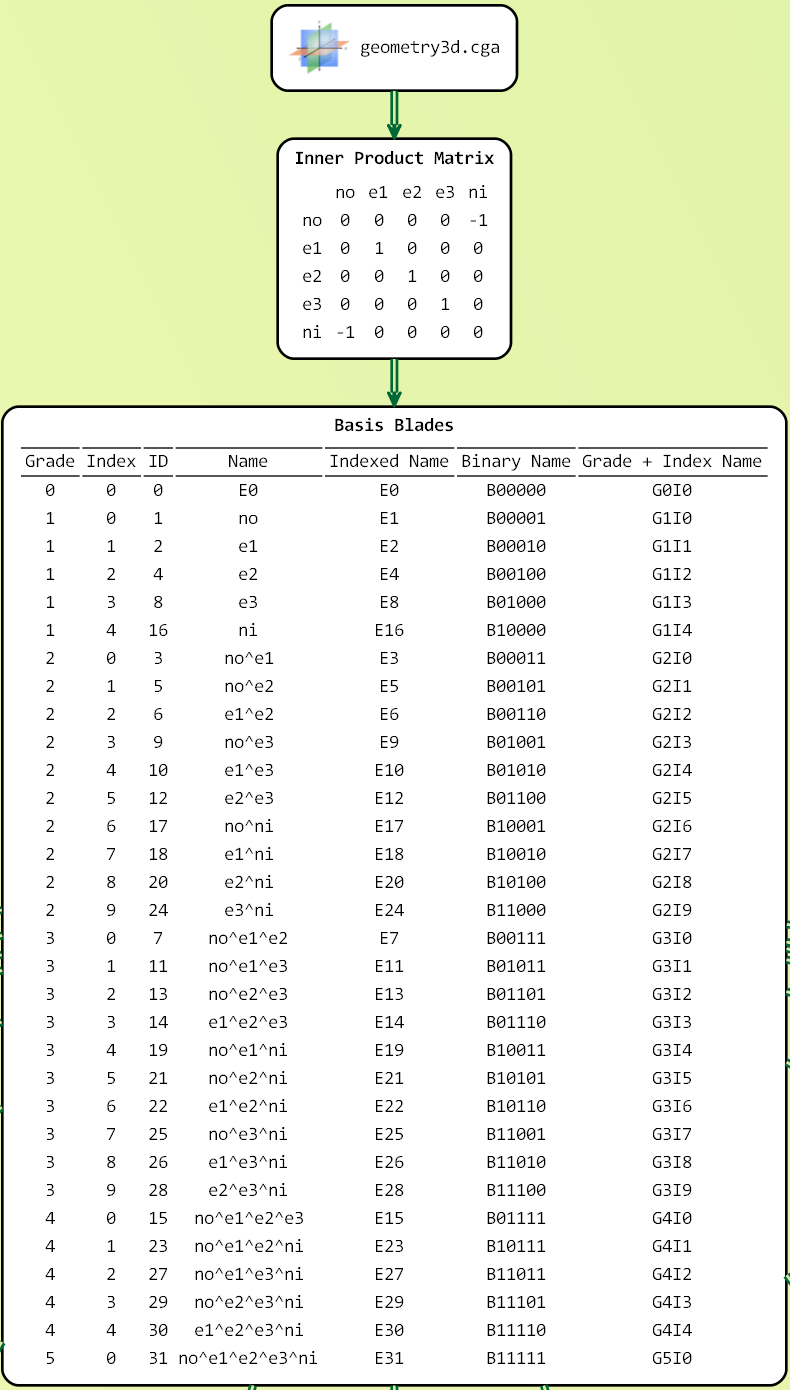
Following the MathematicaExpression wrapper class hierarchy we explained before, GMac has a set of wrapper classes to represent GA frames, multivectors and outermorphisms. Mathematically, a geometric algebra can be constructed from a real vector space and a symmetric bilinear form to define the metric used to compare vectors and associate geometric properties with them like lengths and angles. Using GA’s coordinate-free relations we can create many compact and geometrically significant models and algorithms for scientific and engineering applications. Implementing GA is, however, coordinate dependent because computers basically deal with real numbers and coordinates relate the abstract multivectors to the concrete real numbers. To make that link we define a Frame which is an ordered set of basis vectors for the vector space extended by the Outer Product into an ordered set of basis blades for the geometric algebra. An infinite number of frames can represent the same GA just like a single vector space can be spanned by an infinite number of basis sets. Each frame is based on n linearly independent vectors to construct a 2n dimensional geometric algebra. The n vectors relate to each other using a symmetric Inner-Product Matrix that defines the bilinear form of the GA space. A multivector is simply represented as a linear combination of the frame’s basis blades. All operations on multivectors like the geometric product, outer product, inner products, reverse, etc. can be performed using this simple additive form of multivectors on the selected frame. More details can be found in my introduction to the topic here.

2.1. Representing Basis Blades in GMac

In geometric algebra, a blade of grade k is the outer product of k linearly independent vectors. If we start with an ordered set of basis vectors, a basis blade is the outer product of any selected subset of the basis vectors set. This relation between ordered sets of basis vectors and basis blades can be implemented using a simple binary integer scheme where each basis blade has a unique ID from 0 to 2^n-1. If we represent a basis blade’s ID as binary numbers of n-bits, we can find the basis vectors that comprise the basis blades as the positions containing 1’s in the binary ID. This scheme is used by other GA-related software to implement basis blades inside the computer memory.

In GMac we can find many bit-wise operations on integers implemented under the GMac.GMacUtils.BitUtils static utility class. These utility operations are the lowest-level implementation related to GA in GMac.

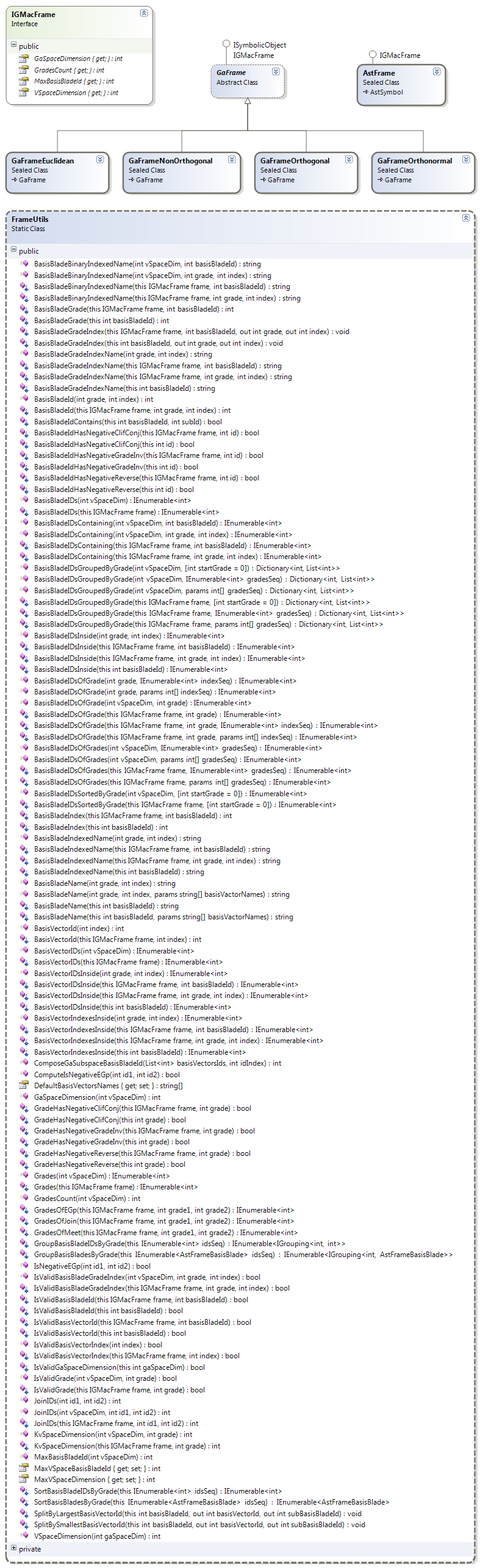
Based on the bit operations, the FrameUtils class contains many operations related to general GA frames. In addition, GMac contains some classes implementing an interface called IGMacFrame. The IGMacFrame interface is implemented by the AstFrame class, described in the GMacAST Guide, and the GaFrame abstract class described in the next sub-section. This interface has many extension methods in the FrameUtils static class to query important properties of GA frames like its GA space dimension, a list of grades its blades can have, the IDs of its basis blades and much more.

 

2.2. Representing GA Frames and Multivectors in GMac

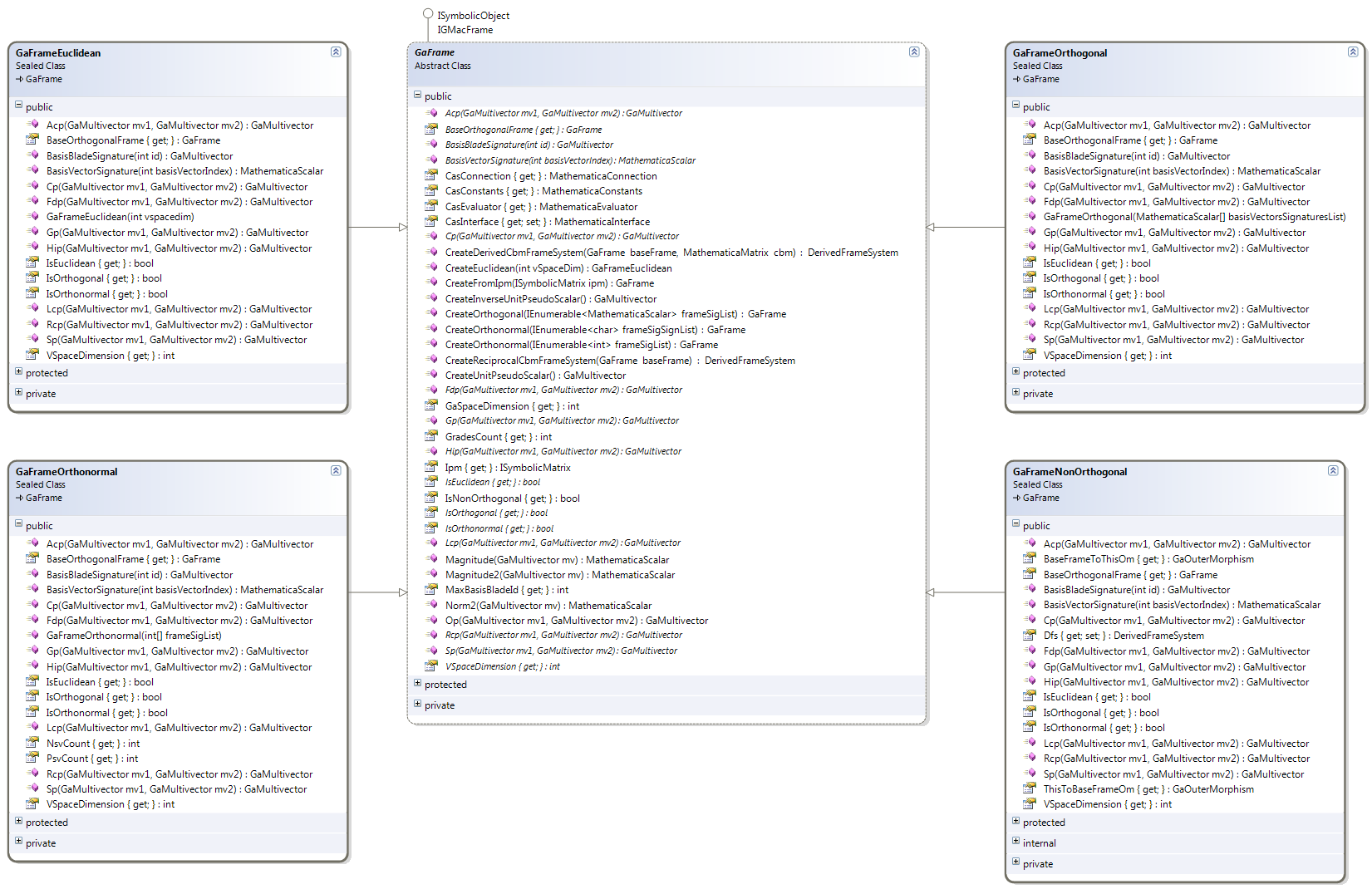
The GaFrame abstract class under the GMac.GMacCompiler.Symbolic.Frame namespace is the base of GA frames implementation in GMac. For any GA frame, we need to define its basis vectors in terms of their number and inner products. The InnerProductMatrix member contains a square symmetric matrix holding this information for all kinds of GA frames. Four derived frame classes are implemented in GMac:

1. GaFrameEuclidean : This class represents a GA frame having any dimension with Euclidean signature. The inner product matrix is always the square unity matrix.
2. GaFrameOrthonormal : This class represents a GA frame with orthonormal signature. An orthonormal signature means that the inner product of any two different basis vectors is 0, and any basis vector with itself is 1 or -1, but not any other value. Euclidean GA frames are a special kind of orthonormal frames.
3. GaFrameOrthogonal : Similar to orthonormal frames but the inner product of a basis vector with itself is any non-zero real number. Orthonormal frames are a special case of orthogonal frames.
4. GaFrameNonOrthogonal : The most general kind of frames with a general symmetric inner product matrix. This kind is very useful for non Euclidean geometry but is computationally expensive to implement manually relative to the other kinds.

For more information about how to use frames and multivectors in GMac see the GMacDSL Guide and the GMacAST Guide.

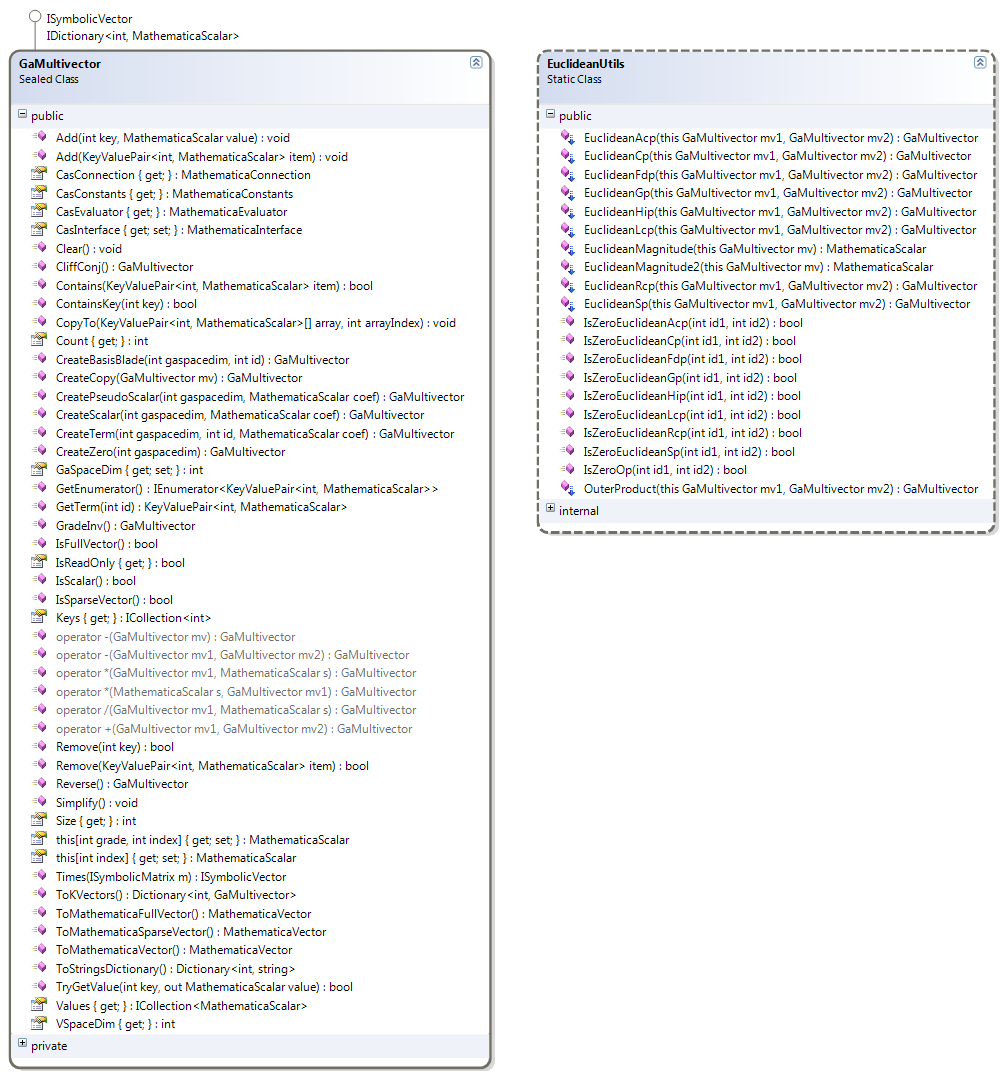
A multivector is a linear combination of basis blades defined in some frame. Many useful multivectors are sparse; most basis blades have a zero coefficient. This is why GMac uses a simple dictionary to represent a GA multivector. The GaMultivector class is the implementation of symbolic GA multivectors that implements the interface IDictionary<int, MathematicaScalar>. The information about the symbolic GA frame the multivector belongs to is not stored in the GaMultivector class itself. The GaMultivector class is just a container of sparse coefficients. This frame information is outside the multivector objects to enable more flexibility while computing.

Many operations on multivectors are independent of the frame, like addition, subtraction, outer product, multiplication by scalars, reverse, grade involution, and component extraction. For these operations, we find methods in the GaMultivector class to implement them. For the frame-dependent operations like geometric product and contractions, we use the frame methods to get the results. The EuclideanUtils static class under the GMac.GMacUtils namespace contains some extension methods to compute products on multivectors assuming a Euclidean metric.

2.3. Representing Linear Transforms on Multivectors in GMac

A geometric algebra is actually a vector space of high dimension. Multivectors can be seen as linear combination of linearly independent basis blades satisfying all axioms of a classic abstract vector space. this is why all linear operations on multivectors are representable as matrices. A general Linear Transformation (LT) on multivectors is represented in GMac as a matrix with an arbitrary structure that transforms a multivector between two frames linearly. The GaLinearTransform class under the GMac.GMacCompiler.Symbolic.GALT namespace is the base class implementing general LTs on multivectors.

One very important special kind of multivector LTs is the Outermorphism (OM). An OM is a generalization of a LT on the basis vectors that preserves the grades of the blades it transforms. A general LT can transform a 2-blade into a 3-blade while an OM can only transform blades to same grade blades. This fundamental property of OMs has many useful applications. The GaOuterMorphism class under the GMac.GMacCompiler.Symbolic.GAOM namespace is derived from the GaLinearTransform class to implement symbolic OMs in GMac infrastructure.