In this guide we will explore GMac scripting by covering the following:
1. GMac Scripting by Example
GMac scripting is essentially based on writing C# code that calls GMac and Mathematica services through a set of subroutines (methods). Some syntactic sugar is used to simplify the common GMac scripting tasks. C# is a, quite big, general purpose object oriented language. However, scripting with C# doesn’t require the use of its full power. Just a bit of variable declarations, arrays, loops, conditions, and expressions is enough for many purposes. The Core C# and .NET Quick Reference is a good place to start. More details can be found in this excellent C# Tutorial. If you need to use the beautiful Linq to objects feature in your scripts, which I highly recommend for complex tasks, read a copy of Troy Magennis’s book “LINQ to Objects Using C# 4.0: Using and Extending LINQ to Objects and Parallel LINQ (PLINQ)“. For more in-depth understanding of C# you can read “Illustrated C# 2012” by Daniel Solis and “C# 4.0 in a Nutshell: The Definitive Reference Fourth Edition” by Joseph Albahari and Ben Albahari.
Wolfram Mathematica is a huge symbolic computer algebra system with many years of developments. To learn Mathematica you need to experiment with specific tasks in mind. Several online quick references exist like this and this. A huge list of Mathematica recipes by Nasser M. Abbasi can be found here and here. You can always go to the online comprehinsive help system for detailed information. In addition, several good books can be found here.
In this section, we will see examples for various tasks coded as GMac scripts and in the following section, we will give a detailed explanation of the GMac scripting engine to fully understand and utilize its capabilities. We will assume the following GMacDSL code is used and compiled into a GMacAST as described in the GMacAST Guide:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
namespace common template macro versorInverse( mv : Multivector) : Multivector begin let b = reverse( mv ) let a = mv gp b return b / a.#E0# end namespace geometry2d frame cgaOrtho (ep, e1, e2, en) orthonormal '+++-' frame cga (no, e1, e2, ni) CBM cgaOrtho @" { {1/2, 0, 0, 1/2}, { 0, 1, 0, 0}, { 0, 0, 1, 0}, { -1, 0, 0, 1} }" open common implement versorInverse using cgaOrtho, cga macro cga.rotate(mv : Multivector, angle : scalar) : Multivector begin let V = 'Cos[$ angle/2 $]' - 'Sin[$ angle/2 $]' * (e1^e2) return V gp mv gp versorInverse(V) end namespace geometry3d frame cgaOrtho (ep, e1, e2, e3, en) orthonormal '++++-' frame cga (no, e1, e2, e3, ni) CBM cgaOrtho @" { {1/2, 0, 0, 0, 1/2}, { 0, 1, 0, 0, 0}, { 0, 0, 1, 0, 0}, { 0, 0, 0, 1, 0}, { -1, 0, 0, 0, 1} }" |
1.1. Initialization, Input, and Output
The first step in getting familiar with any scripting environment is to know how to initialize the script, how to input data and how to output information. The first line of code in any GMac script should take the following form:
|
1 |
<: "geometry2d.cga" |> Reset :>; |
This command simply tells the GMac script engine to reference any following GMac symbols (frames, constants, structures, macros, etc.) starting from the scope of the geometry2d.cga frame. So for example if we later need to declare a GMac multivector variable under the cga frame we would write declare Mv : Multivector instead of the fully qualified name declare Mv : geometry2d.cga.Multivector.
For our data input and general processing, we can use normal C# variable declaration and initialization syntax in the GMac script. All core C# datatypes are available to the script to use, along with the C# standard operators, decision making statements, looping statements, arrays, string manipulation, file input\output, and many more advanced C# features. The script writer can select whatever is necessary from all C# features from the simple to the complex.
For information output we can use two kinds of reporting mechanisms in the GMac script:
- Use the script’s Log object to report formatted text to the script user. The Log object is of type LinearComposer described in the TextComposerLib Guide.
- Use the script’s Output object to store text, images, or GMac multivector values for later viewing, each value can have its own text title and description string.
For example, the following script displays the even numbers from 1 to 10 to the Log object:
|
1 2 3 4 5 6 7 8 9 10 11 |
for (var i = 2; i <= 10; i += 2) <: i |> AppendAtNewLine :>; /* This will output the text: 2 4 6 8 10 */ |
While the following script will store the same numbers each with its own descriptive title for later viewing:
|
1 2 3 4 5 6 7 8 9 10 |
for (var i = 2; i <= 10; i += 2) <: "I found the even number: ", i |> Store :>; /*This will store the 5 string values I found the even number: 2 I found the even number: 4 I found the even number: 6 I found the even number: 8 I found the even number: 10 */ |
The use of GMac script commands between <: :> delimiters is a simplified syntax that will be internally translated into C# code calling GMac methods as we will explain in the second section in detail. We could have written two previous example as follows and the results will be exactly the same:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//This mixed C# and GMac script command code: for (var i = 2; i <= 10; i += 2) <: i |> AppendAtNewLine :>; //Is the same as this pure C# code: for (var i = 2; i <= 10; i += 2) Ipr.Output.Log.AppendAtNewLine(i); //And this mixed C# and GMac script command code: for (var i = 2; i <= 10; i += 2) <: "I found the even number: ", i |> Store :>; //Is the same as this pure C# code: for (var i = 2; i <= 10; i += 2) Ipr.Output.Store("I found the even number: ", i); |
1.2. Using GMacAST Data in the Script
The GMac script engine is initialized using a GMacAST structure compiled from GMacDSL code, like the code in the beginning of this guide. The script user can access any information in the GMacAST using members and methods described in full details in the GMacAST Guide.
The following script will display the qualified names for namespaces, frames, and macros in our compiled GMacAST. Here we use the Root member (the same as the Ipr.Root member) that directly points to the AstRoot object of the compiled GMacAST:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 |
<: "common" |> reset :>; <: "Namespaces: " |> AppendNewLine :>; foreach (var nameSpace in Root.Namespaces) <: " " + nameSpace.AccessName |> AppendNewLine :>; <: |> AppendNewLine :>; <: "Frames: " |> AppendNewLine :>; foreach (var frame in Root.Frames) <: " " + frame.AccessName |> AppendNewLine :>; <: |> AppendNewLine :>; <: "Macros: " |> AppendNewLine :>; foreach (var macro in Root.Macros) <: " " + macro.AccessName |> AppendNewLine :>; /* This will display: Namespaces: common geometry2d geometry3d Frames: geometry2d.cgaOrtho geometry2d.cga geometry3d.cgaOrtho geometry3d.cga Macros: geometry2d.cgaOrtho.Mag geometry2d.cgaOrtho.Mag2 geometry2d.cgaOrtho.Norm2 geometry2d.cgaOrtho.InvVersor geometry2d.cgaOrtho.Dual geometry2d.cgaOrtho.SelfGP geometry2d.cgaOrtho.SelfGPRev geometry2d.cgaOrtho.Negative geometry2d.cgaOrtho.Reverse geometry2d.cgaOrtho.GradeInv geometry2d.cgaOrtho.CliffConj geometry2d.cgaOrtho.EMag geometry2d.cgaOrtho.EMag2 geometry2d.cgaOrtho.InvEVersor geometry2d.cgaOrtho.EDual geometry2d.cgaOrtho.SelfEGP geometry2d.cgaOrtho.SelfEGPRev geometry2d.cgaOrtho.SP geometry2d.cgaOrtho.GP geometry2d.cgaOrtho.LCP geometry2d.cgaOrtho.RCP geometry2d.cgaOrtho.FDP geometry2d.cgaOrtho.HIP geometry2d.cgaOrtho.CP geometry2d.cgaOrtho.ACP geometry2d.cgaOrtho.GPDual geometry2d.cgaOrtho.DWP geometry2d.cgaOrtho.GWP geometry2d.cgaOrtho.Times geometry2d.cgaOrtho.Divide geometry2d.cgaOrtho.OP geometry2d.cgaOrtho.ESP geometry2d.cgaOrtho.EGP geometry2d.cgaOrtho.ELCP geometry2d.cgaOrtho.ERCP geometry2d.cgaOrtho.EFDP geometry2d.cgaOrtho.EHIP geometry2d.cgaOrtho.ECP geometry2d.cgaOrtho.EACP geometry2d.cgaOrtho.EGPDual geometry2d.cgaOrtho.EDWP geometry2d.cgaOrtho.EGWP geometry2d.cgaOrtho.ApplyLT geometry2d.cgaOrtho.TransLT geometry2d.cgaOrtho.ComposeLT geometry2d.cgaOrtho.AddLT geometry2d.cgaOrtho.SubtractLT geometry2d.cgaOrtho.TimesLT geometry2d.cgaOrtho.DivideLT geometry2d.cgaOrtho.OMToLT geometry2d.cgaOrtho.ApplyOM geometry2d.cgaOrtho.AVOM geometry2d.cgaOrtho.TransOM geometry2d.cgaOrtho.DetOM geometry2d.cgaOrtho.EDetOM geometry2d.cgaOrtho.ComposeOM geometry2d.cgaOrtho.AddOM geometry2d.cgaOrtho.SubtractOM geometry2d.cgaOrtho.TimesOM geometry2d.cgaOrtho.DivideOM geometry2d.cgaOrtho.VersorToOM geometry2d.cgaOrtho.VersorToLT geometry2d.cgaOrtho.ApplyVersor geometry2d.cgaOrtho.ApplyRotor geometry2d.cgaOrtho.ApplyReflector geometry2d.cgaOrtho.EVersorToOM geometry2d.cgaOrtho.EVersorToLT geometry2d.cgaOrtho.ApplyEVersor geometry2d.cgaOrtho.ApplyERotor geometry2d.cgaOrtho.ApplyEReflector geometry2d.cgaOrtho.versorInverse geometry2d.cga.Mag geometry2d.cga.Mag2 geometry2d.cga.Norm2 geometry2d.cga.InvVersor geometry2d.cga.Dual geometry2d.cga.SelfGP geometry2d.cga.SelfGPRev geometry2d.cga.Negative geometry2d.cga.Reverse geometry2d.cga.GradeInv geometry2d.cga.CliffConj geometry2d.cga.EMag geometry2d.cga.EMag2 geometry2d.cga.InvEVersor geometry2d.cga.EDual geometry2d.cga.SelfEGP geometry2d.cga.SelfEGPRev geometry2d.cga.SP geometry2d.cga.GP geometry2d.cga.LCP geometry2d.cga.RCP geometry2d.cga.FDP geometry2d.cga.HIP geometry2d.cga.CP geometry2d.cga.ACP geometry2d.cga.GPDual geometry2d.cga.DWP geometry2d.cga.GWP geometry2d.cga.Times geometry2d.cga.Divide geometry2d.cga.OP geometry2d.cga.ESP geometry2d.cga.EGP geometry2d.cga.ELCP geometry2d.cga.ERCP geometry2d.cga.EFDP geometry2d.cga.EHIP geometry2d.cga.ECP geometry2d.cga.EACP geometry2d.cga.EGPDual geometry2d.cga.EDWP geometry2d.cga.EGWP geometry2d.cga.ApplyLT geometry2d.cga.TransLT geometry2d.cga.ComposeLT geometry2d.cga.AddLT geometry2d.cga.SubtractLT geometry2d.cga.TimesLT geometry2d.cga.DivideLT geometry2d.cga.OMToLT geometry2d.cga.ApplyOM geometry2d.cga.AVOM geometry2d.cga.TransOM geometry2d.cga.DetOM geometry2d.cga.EDetOM geometry2d.cga.ComposeOM geometry2d.cga.AddOM geometry2d.cga.SubtractOM geometry2d.cga.TimesOM geometry2d.cga.DivideOM geometry2d.cga.VersorToOM geometry2d.cga.VersorToLT geometry2d.cga.ApplyVersor geometry2d.cga.ApplyRotor geometry2d.cga.ApplyReflector geometry2d.cga.EVersorToOM geometry2d.cga.EVersorToLT geometry2d.cga.ApplyEVersor geometry2d.cga.ApplyERotor geometry2d.cga.ApplyEReflector geometry2d.cga.versorInverse geometry2d.cga.rotate geometry3d.cgaOrtho.Mag geometry3d.cgaOrtho.Mag2 geometry3d.cgaOrtho.Norm2 geometry3d.cgaOrtho.InvVersor geometry3d.cgaOrtho.Dual geometry3d.cgaOrtho.SelfGP geometry3d.cgaOrtho.SelfGPRev geometry3d.cgaOrtho.Negative geometry3d.cgaOrtho.Reverse geometry3d.cgaOrtho.GradeInv geometry3d.cgaOrtho.CliffConj geometry3d.cgaOrtho.EMag geometry3d.cgaOrtho.EMag2 geometry3d.cgaOrtho.InvEVersor geometry3d.cgaOrtho.EDual geometry3d.cgaOrtho.SelfEGP geometry3d.cgaOrtho.SelfEGPRev geometry3d.cgaOrtho.SP geometry3d.cgaOrtho.GP geometry3d.cgaOrtho.LCP geometry3d.cgaOrtho.RCP geometry3d.cgaOrtho.FDP geometry3d.cgaOrtho.HIP geometry3d.cgaOrtho.CP geometry3d.cgaOrtho.ACP geometry3d.cgaOrtho.GPDual geometry3d.cgaOrtho.DWP geometry3d.cgaOrtho.GWP geometry3d.cgaOrtho.Times geometry3d.cgaOrtho.Divide geometry3d.cgaOrtho.OP geometry3d.cgaOrtho.ESP geometry3d.cgaOrtho.EGP geometry3d.cgaOrtho.ELCP geometry3d.cgaOrtho.ERCP geometry3d.cgaOrtho.EFDP geometry3d.cgaOrtho.EHIP geometry3d.cgaOrtho.ECP geometry3d.cgaOrtho.EACP geometry3d.cgaOrtho.EGPDual geometry3d.cgaOrtho.EDWP geometry3d.cgaOrtho.EGWP geometry3d.cgaOrtho.ApplyLT geometry3d.cgaOrtho.TransLT geometry3d.cgaOrtho.ComposeLT geometry3d.cgaOrtho.AddLT geometry3d.cgaOrtho.SubtractLT geometry3d.cgaOrtho.TimesLT geometry3d.cgaOrtho.DivideLT geometry3d.cgaOrtho.OMToLT geometry3d.cgaOrtho.ApplyOM geometry3d.cgaOrtho.AVOM geometry3d.cgaOrtho.TransOM geometry3d.cgaOrtho.DetOM geometry3d.cgaOrtho.EDetOM geometry3d.cgaOrtho.ComposeOM geometry3d.cgaOrtho.AddOM geometry3d.cgaOrtho.SubtractOM geometry3d.cgaOrtho.TimesOM geometry3d.cgaOrtho.DivideOM geometry3d.cgaOrtho.VersorToOM geometry3d.cgaOrtho.VersorToLT geometry3d.cgaOrtho.ApplyVersor geometry3d.cgaOrtho.ApplyRotor geometry3d.cgaOrtho.ApplyReflector geometry3d.cgaOrtho.EVersorToOM geometry3d.cgaOrtho.EVersorToLT geometry3d.cgaOrtho.ApplyEVersor geometry3d.cgaOrtho.ApplyERotor geometry3d.cgaOrtho.ApplyEReflector geometry3d.cga.Mag geometry3d.cga.Mag2 geometry3d.cga.Norm2 geometry3d.cga.InvVersor geometry3d.cga.Dual geometry3d.cga.SelfGP geometry3d.cga.SelfGPRev geometry3d.cga.Negative geometry3d.cga.Reverse geometry3d.cga.GradeInv geometry3d.cga.CliffConj geometry3d.cga.EMag geometry3d.cga.EMag2 geometry3d.cga.InvEVersor geometry3d.cga.EDual geometry3d.cga.SelfEGP geometry3d.cga.SelfEGPRev geometry3d.cga.SP geometry3d.cga.GP geometry3d.cga.LCP geometry3d.cga.RCP geometry3d.cga.FDP geometry3d.cga.HIP geometry3d.cga.CP geometry3d.cga.ACP geometry3d.cga.GPDual geometry3d.cga.DWP geometry3d.cga.GWP geometry3d.cga.Times geometry3d.cga.Divide geometry3d.cga.OP geometry3d.cga.ESP geometry3d.cga.EGP geometry3d.cga.ELCP geometry3d.cga.ERCP geometry3d.cga.EFDP geometry3d.cga.EHIP geometry3d.cga.ECP geometry3d.cga.EACP geometry3d.cga.EGPDual geometry3d.cga.EDWP geometry3d.cga.EGWP geometry3d.cga.ApplyLT geometry3d.cga.TransLT geometry3d.cga.ComposeLT geometry3d.cga.AddLT geometry3d.cga.SubtractLT geometry3d.cga.TimesLT geometry3d.cga.DivideLT geometry3d.cga.OMToLT geometry3d.cga.ApplyOM geometry3d.cga.AVOM geometry3d.cga.TransOM geometry3d.cga.DetOM geometry3d.cga.EDetOM geometry3d.cga.ComposeOM geometry3d.cga.AddOM geometry3d.cga.SubtractOM geometry3d.cga.TimesOM geometry3d.cga.DivideOM geometry3d.cga.VersorToOM geometry3d.cga.VersorToLT geometry3d.cga.ApplyVersor geometry3d.cga.ApplyRotor geometry3d.cga.ApplyReflector geometry3d.cga.EVersorToOM geometry3d.cga.EVersorToLT geometry3d.cga.ApplyEVersor geometry3d.cga.ApplyERotor geometry3d.cga.ApplyEReflector */ |
The following script will display the names of all basis blades in the geometry2d.cga frame ordered by their grade. To reference a GMacAST symbol by its name we can use the GMac script commands frame, namespace, macro, structure, etc. These commands will return a reference for the symbol’s AST node object. More about these commands in the second section of this guide:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
//Reset GMac scripting main engine scope <: "geometry2d.cga" |> reset:>; //Get AST information of the geometry2d.cga frame var cgaFrameInfo = <: "cga" |> frame :>; //Display Canonical names of all basis blades in the frame foreach (var basisBladeInfo in cgaFrameInfo.BasisBladesSortedByGrade()) <: basisBladeInfo.Name |> AppendNewLine :>; /* This will display: E0 no e1 e2 ni no^e1 no^e2 e1^e2 no^ni e1^ni e2^ni no^e1^e2 no^e1^ni no^e2^ni e1^e2^ni no^e1^e2^ni */ |
1.3. Computing with GMac Commands and Expressions
Now we come to the interesting part: how to compute with multivectors in a GMac script. The method is very simple, just pass a string containing GMac declare and let commands to a script command called Execute, also Exec for short, and GMac will create its own local variables and compute values from GMacDSL expressions and assign them to the GMac local variables. The GMac local variables are completely separate from the C# local variables in the main script, so you can use the same names, although this might reduce readability of your script. At any time after executing the commands you can query values of GMac local variables, or any part of them, using the ValueOf script command. You can also evaluate GMac expressions without assigning them to GMac local variables using the Evaluate script command. This technique is intended to close the gap between the non-Turing complete GMacDSL code and typical scripting requirements using the full power of C# syntax.
For example this script verifies a geometric algebra identity in a vector and a blade in the geometry3d.cga frame:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
//Verify the GA identity c ^ X == (c gp X + grade_inv(X) gp c) / 2 //on the given symbolic vector c and 2-blade X //Set main scope [: geometry3d.cga |> reset :]; //Execute some GMac commands [: let a = Multivector(#e1# = 'ax', #e2# = 'ay', #e3# = 'az') let b = Multivector(#e1# = 'bx', #e2# = 'by', #e3# = 'bz') let c = Multivector(#e1# = 'cx', #e2# = 'cy', #e3# = 'cz') let X = a ^ b |> exec :]; //Output the values of local GMac variables a, b, c, and X [: a = |> Append :]; [: a |> ValueOf |> AsString |> AppendLine :]; [: b = |> Append :]; [: b |> ValueOf |> AsString |> AppendLine :]; [: c = |> Append :]; [: c |> ValueOf |> AsString |> AppendLine :]; [: X = |> Append :]; [: X |> ValueOf |> AsString |> AppendLine :]; [: |> AppendLine :]; //Evaluate and output values of both sides of the identity and the difference between them [: c ^ X = |> Append :]; [: c ^ X |> Evaluate |> AsString |> AppendLine :]; [: (c gp X + grade_inv(X) gp c) / 2 = |> Append :]; [: (c gp X + grade_inv(X) gp c) / 2 |> Evaluate |> AsString |> AppendLine :]; [: |> AppendLine :]; [: Difference = |> Append :]; [: c ^ X - (c gp X + grade_inv(X) gp c) / 2 |> Evaluate |> AsString |> AppendLine :]; /* This should give the text result: a = ax e1 + ay e2 + az e3 b = bx e1 + by e2 + bz e3 c = cx e1 + cy e2 + cz e3 X = Plus[Times[-1,ay,bx],Times[ax,by]] e1^e2 + Plus[Times[-1,az,bx],Times[ax,bz]] e1^e3 + Plus[Times[-1,az,by],Times[ay,bz]] e2^e3 c ^ X = Plus[Times[-1,az,by,cx],Times[ay,bz,cx],Times[az,bx,cy],Times[-1,ax,bz,cy],Times[-1,ay,bx,cz],Times[ax,by,cz]] e1^e2^e3 (c gp X + grade_inv(X) gp c) / 2 = Plus[Times[-1,az,by,cx],Times[ay,bz,cx],Times[az,bx,cy],Times[-1,ax,bz,cy],Times[-1,ay,bx,cz],Times[ax,by,cz]] e1^e2^e3 Difference = 0 */ |
First of all this code contains many lines with GMac script commands on the form [: argument |> ValueOf |> AsString |> AppendLine :]. These are examples for composition of GMac commands where the result of the ValueOf command is passed to the AsString command then to the AppendLine command.
The lines 8:16 from the script request the creation of 4 local multivector variables (inside GMac not C#): a, b, c, and X, and assign certain symbolic values for a, b, and c while computing X from a and b using a simple GMac expression. The script then outputs the values of the 4 GMac local variables using the ValueOf and AsString GMac script commands. Finally several expressions are evaluated and displayed using the Evaluate command.
One other thing about this script is the use of GMac script commands delimited by [: :] rather than <: :>. This is another syntax simplification that can reduce script code like this:
|
1 2 3 4 5 6 7 8 |
<: @" let a = Multivector(#e1# = 'ax', #e2# = 'ay', #e3# = 'az') let b = Multivector(#e1# = 'bx', #e2# = 'by', #e3# = 'bz') let c = Multivector(#e1# = 'cx', #e2# = 'cy', #e3# = 'cz') let X = a ^ b " |> exec :>; |
Into the simpler equivalent script code:
|
1 2 3 4 5 6 7 8 9 |
[: let a = Multivector(#e1# = 'ax', #e2# = 'ay', #e3# = 'az') let b = Multivector(#e1# = 'bx', #e2# = 'by', #e3# = 'bz') let c = Multivector(#e1# = 'cx', #e2# = 'cy', #e3# = 'cz') let X = a ^ b |> exec :]; |
The [: :] syntax is called a square bracket command while the <: :> syntax is an angle bracket command, and we can mix them in a single script as needed. More details on the differences between the two in the second section of this guide.
Another example is the following script that will produce the inner product matrix of basis vectors for the selected frame:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
//Generate the inner product matrix for some given frame //Set main scope [:geometry2d.cga |> reset:]; //Initialize C# local variables: //Get information of the geometry2d.cga frame from GMacAST var cgaFrameInfo = [:cga |> frame:]; //Read the vector space dimension of the geometry2d.cga frame (= 4) var n = cgaFrameInfo.VSpaceDimension; //Create a list of basis vector IDs for the geometry2d.cga frame (= {1, 2, 4, 8}) var ids = cgaFrameInfo.BasisVectorIDs().ToArray(); //Initialize the table holding the result var table = new string[n + 1, n + 1]; var r = 0; foreach (var id1 in ids) { //Fill title row, column to hold names of basis vectors var basisVectorName = cgaFrameInfo.BasisVectorFromIndex(r).Name; table[r + 1, 0] = basisVectorName; table[0, r + 1] = basisVectorName; var c = 0; foreach (var id2 in ids) { //Each cell in the table is the scalar product of two basis vectors converted into a string value table[r+1, c+1] = [: Multivector(#E|{id1}|# = 1) sp Multivector(#E|{id2}|# = 1) |> Evaluate |> AsString :>; c++; } r++; } //Display the final result <: "Inner Product Matrix:" |> AppendLine :>; <: table.FormatAsTable() |> AppendLine :>; /* This will output: Inner Product Matrix: no e1 e2 ni no 0 0 0 -1 e1 0 1 0 0 e2 0 0 1 0 ni -1 0 0 0 */ |
Most of the script is clear, I hope, but we need to comment on the code in line 30 that I will re-write in the equivalent angle bracket syntax:
|
1 |
table[r+1, c+1] = <: "| Multivector(#E|{id1}|# = 1) sp Multivector(#E|{id2}|# = 1) |" |> Evaluate |> AsString :>; |
The argument is a parametric string surrounded by "| |" delimiters. Inside the parametric string we see some text blocks surrounded by the |{ }| delimiters (in this example |{id1}| and |{id2}|). The GMac scripting engine recognizes this format and replaces the |{ }| delimited blocks by the C# expressions inside them, functionally equivalent to a concatenation of several strings and values. This is a very useful shorthand to enable the script user to construct GMac code to be executed based on C# expressions. Effectively the two loops in the script request the evaluation of these 16 GMac expressions, see the multivector constructor expression in the GMacDSL Guide for more details:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Multivector(#E1# = 1) sp Multivector(#E1# = 1) Multivector(#E1# = 1) sp Multivector(#E2# = 1) Multivector(#E1# = 1) sp Multivector(#E4# = 1) Multivector(#E1# = 1) sp Multivector(#E8# = 1) Multivector(#E2# = 1) sp Multivector(#E1# = 1) Multivector(#E2# = 1) sp Multivector(#E2# = 1) Multivector(#E2# = 1) sp Multivector(#E4# = 1) Multivector(#E2# = 1) sp Multivector(#E8# = 1) Multivector(#E4# = 1) sp Multivector(#E1# = 1) Multivector(#E4# = 1) sp Multivector(#E2# = 1) Multivector(#E4# = 1) sp Multivector(#E4# = 1) Multivector(#E4# = 1) sp Multivector(#E8# = 1) Multivector(#E8# = 1) sp Multivector(#E1# = 1) Multivector(#E8# = 1) sp Multivector(#E2# = 1) Multivector(#E8# = 1) sp Multivector(#E4# = 1) Multivector(#E8# = 1) sp Multivector(#E8# = 1) |
1.4. Using Mathematica for Additional Tasks
One important feature of the GMac scripting engine is the ability to execute Mathemetica’s symbolic text code using commands similar to the ones we used when executing GMac code. We can always use Mathematica to create symbolic values and then assign the values to the scalar coefficients of GMac multivectors or scalar members of GMac structures. We can also use the GMac value components as inputs to some Mathematica symbolic manipulation algorithm; C# gluing everything together.
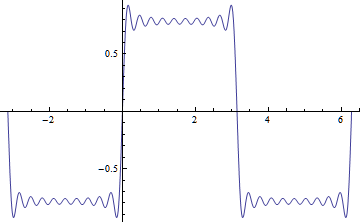
The following is an example for plotting the results of a script using Mathematica’s Plot[] function:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//Square wave approximation by geometric operations [:geometry2d.cga |> reset:]; //Initialize GMac multivector variables [: let angle = 't' let unit = Multivector(#e1# = 1) declare signalMv : Multivector |> exec :]; //Construct rotated vectors and add them together to form a multivector signal for (var i = 1; i <= 20; i += 2) [: let signalMv = signalMv + rotate(unit, |{i}| * angle) / |{i}| |> exec :]; //Project multivector signal on vertical axis to get scalar signal. //Then format signal equation using Mathematica var signal = [: signalMv.#e2# |> ValueOf |> AsString |> ComputeToInputForm :]; //Display the symbolic equation of the signal <: signal |> AppendLine :>; //Plot signal between -2 Pi and 2 Pi using Mathematica into a C# System.Drawing.Image object var img = [: Plot[ |{signal}| , {t, -Pi, 2 Pi}] |> ComputeToImage :]; //Save the C# Image object into a file img.Save(@"C:\GMac\fs.bmp"); |
The ComputeToInputForm and ComputeToImage commands take a string containing a Mathematica expression or code and return a C# string and an C# Image object respectively. The equation found by this script is:
|
1 |
Sin[t] + Sin[3*t]/3 + Sin[5*t]/5 + Sin[7*t]/7 + Sin[9*t]/9 + Sin[11*t]/11 + Sin[13*t]/13 + Sin[15*t]/15 + Sin[17*t]/17 + Sin[19*t]/19 |
And the plotted signal is:
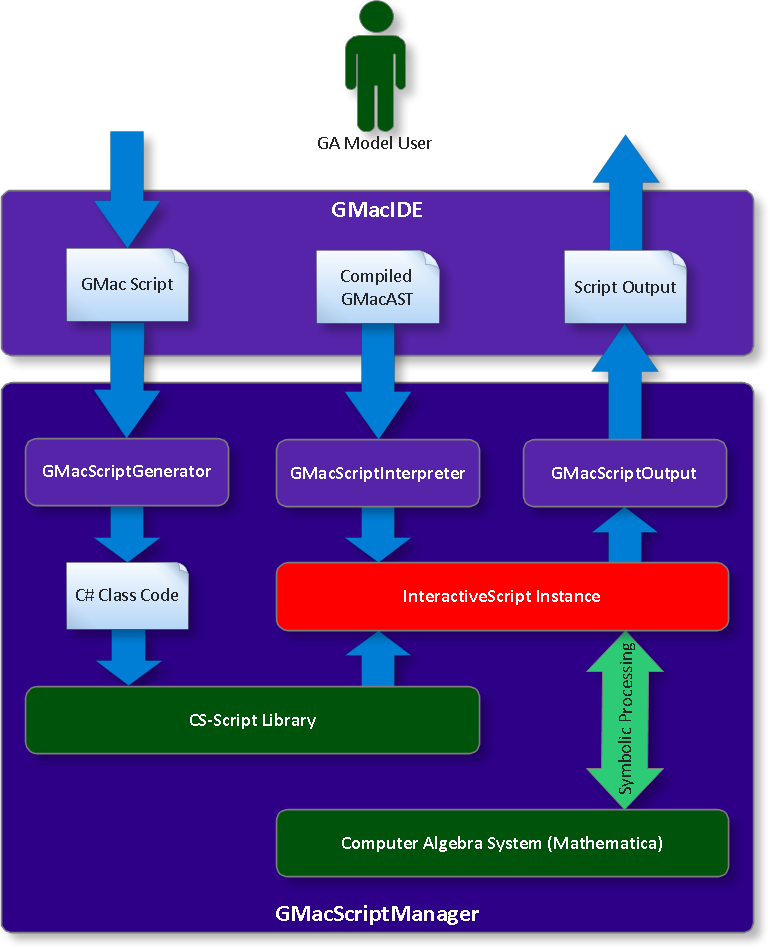
2. GMac Scripting: The Full Picture
GMac scripting is intended for exploration of geometric ideas through GA-based geometric models and algorithms. Three languages can be integrated into a single GMac script, each for a specific purpose:
- C# code comprises the main body of the script. C# is not originally designed for scripting purposes, nevertheless, C# is a very powerful compiled statically typed object-oriented language that can be used for scripting. To simplify using C# as a scripting interface for GMac some syntactic sugar is used to “sweeten” the process of reading and writing GMac scripts.
- GMacDSL code can be executed on multivector values and structures. The scalar coefficients of multivectors can be numerical, symbolic, or a mix of both. GMac code is passed, as C# public method calls, to GMac internal services in string form to be automatically compiled and executed by GMac. The most important GMacDSL elements in use are the let and declare commands and all kinds of multivector expressions described in detail in the GMacDSL Guide.
- Mathematica code can be executed on the Mathematica kernel used in the background by GMac. The Mathematica text code is passed through C# service method calls to the Mathematica kernel. This can be used to exploit the full power of Mathematica through GMac to perform many symbolic manipulations and graphing tasks related to the purpose of the GA-based script exploration.
The main input to the script is always a GMacAST structure compiled from the main GMacDSL code. Detailed information of GMacAST symbols, like frames, basis blades, constants, structures, and macros, are accessible through the script’s Root object. The combination of GMacAST structure, C#, GMac, and Mathematica code, make GMac scripting a very powerful method for GA-models exploration from the very simple to the very complex.
Scripting in GMac is not intended for efficient execution of GA-based algorithms. If the user is satisfied by the final algorithm, GMacAPI can be used by a good software designer to implement an efficient, well-structured version of the script in any desired programming language, with specific types of multivectors and GA algorithms. See the GMacAPI and TextComposerLib Guides for more details on efficient GA-based code generation in GMac.
2.1. The Base: CS-Script Library
The library on which GMac scripting is based is called CS-Script, that I found having many features suitable for GMac scripting. In Wikipedia the library is described as:
CS-Script is a CLR (Common Language Runtime) based scripting system which uses ECMA-compliant C# as a programming language. CS-Script currently targets Microsoft implementation of CLR (.NET 2.0/3.0/3.5/4.0) and with full support for Mono. CS-Script is a statically typed language and it allows unlimited access to .NET/CLR functionality with plain vanilla C# syntax. CS-Script as a scripting environment offers stand alone script execution as well as hosting the script engine from CLR application. Because of statically typed nature of the script execution, CS-Script demonstrates no performance degradation comparing to the compiled managed binaries.
When the user enters a GMac Script to be executed, the final step of execution involves passing pure C# code into the CS-Script system. The code is actually a fully generated C# class that implements the following GMac interface:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
public interface IGMacScript { /// <summary> /// The interpreter for the script /// </summary> GMacScriptInterpreter Ipr { get; set; } /// <summary> /// The root of the GMacAST for this script /// </summary> AstRoot Root { get; } /// <summary> /// The code to be executed /// </summary> void Process(); } |
The simplest form, corresponding to a GMac script having no code, of the the passed C# class is as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
using System; using System.Collections.Generic; using System.Linq; using GMac; using GMac.GMacAST; using GMac.GMacAST.Symbols; using GMac.GMacAST.Expressions; using GMac.GMacAST.Commands; using GMac.GMacAPI.Binding; using GMac.GMacScripting; using TextComposerLib; using TextComposerLib.Linear; using Wolfram.NETLink; //The user can select any additional namespaces here to be used //in the InteractiveScript class's code /// <summary> /// This class represents a GMac script to be executed using an internal script interpreter object /// </summary> public sealed class InteractiveScript : IGMacScript { /// <summary> /// The script interpreter object that executes all script commands /// </summary> public GMacScriptInterpreter Ipr { get; set; } /// <summary> /// The root GMacAST for this script /// </summary> public AstRoot Root { get { return Ipr.Root; } } //The user can define additional classes, fields, properties, and methods here //to be used by the code in the Process() method /// <summary> /// The processing code to be executed /// </summary> public void Process() { //The main script code of the user is put here. The user would typically //be using methods of the Ipr class member to call GMac internal services } } |
Several GMac classes under the GMac.GMacScripting namespace collaborate to produce the desired class, initialize an instance, and call its Process() method to execute the script as described in the following sub-sections.
2.2. The Translator: GMacScriptGenerator Class
C# is a great Object Oriented Programming language suitable for creating very complex projects. the CS-Script system enables using C# as a scripting language. Unfortunately the C# syntax is not originally designed for scripting which typically requires simple uncluttered code and small overhead. GMac scripting is based on a simplified set of specially formatted commands that translate into C# code without intervention from the user. This translation is the responsibility of the GMacScriptGenerator class. The sequence of translation steps goes as follows:
1- Square Bracket Commands:
The first step is to translate all square bracket commands. A square bracket command takes the general form:
|
1 |
[: textArgs |> f1 |> f2 |> f3 :] |
This is translated into the following intermediate form:
|
1 |
@f3( @f2( @f1( "| textArgs |" ) ) ) |
Essentially this commands uses a “pipe-forward” syntax to pass the arguments to a composition of methods (similar in meaning to the right composition /* Mathematica operator). In later stages the @f1, @f2, @f3, and "| textArgs |" parts will be processed into correct meaningful C# code parts. We can pipe-forward to any number of methods we need as long as each is defined to take a single argument compatible with the result of the previous command. For example this square bracket command will compile a given string into an AstExpression GMacAST object, evaluate the AstExpression into an AstValue object, convert the AstValue into a string, and finally append the string into a separate line in the output log of the script:
|
1 |
[: (A gp B) gp versorInverse(B) |> expression |> evaluate |> asString |> appendAtNewLine :] |
After translation the command will take the form:
|
1 |
@appendAtNewLine(@asString(@evaluate(@expression("| (A gp B) gp versorInverse(B) |")))) |
Eventually this will be translated into the C# code:
|
1 |
Ipr.Output.Log.AppendAtNewLine(Ipr.AsString(Ipr.Evaluate(Ipr.Expression(@" (A gp B) gp versorInverse(B) ")))) |
If the bracket command has no method names, just the text argument, it will be translated into a string. For example the bracket command [: Sin[ |{i}| ] :] translates into "| Sin[ |{i}| ] |" and eventually into the C# code Ipr.Substitute(" Sin[ |{0}| ] ", i), while the command [: Sin[x] :] eventually translates into the string " Sin[x] " because it has no parameters between |{ }| delimiters.
2- Angle Bracket Commands:
The second step is to translate all angle bracket commands. Angle bracket commands have the general form:
|
1 |
<: arg1, arg2, arg3 |> f1 |> f2 |> f3 :> |
This is translated into the following intermediate form:
|
1 |
@f3( @f2( @f1(arg1, arg2, arg3) ) ) |
The two main differences between square and angle bracket commands are:
- Square bracket commands get translated first, so we can use square bracket commands inside arguments to angle bracket commands safely, but not the other way around. Generally we can’t nest square or angle commands, the only safe combination is to use square bracket commands as arguments to angle bracket commands.
- All text before the first |> operator of the square bracket command get converted into a single string argument, while the arguments of the angle bracket command are left exactly as they are. Angle bracket commands can have multiple arguments before the first pipe-forward operator |> separated by commas.
For example the command <: A, B |> f |> g :> would translate into @g( @h( A, B ) ) while the command [: A, B |> f |> g :] would translate into @g( @h( "| A, B |" ) )
3- Parametric Strings:
The third step is to find all strings on the form "|any text here|" (i.e. string literals starting with "| and ending with |") and replace them by a Ipr.Substitute() method call, functionally equivalent to the C# String.Format() method. Inside the given string if a block of text on the form |{arg}| is found it’s replaced by a numbered placeholder |{n}| in the final Ipr.Substitute() code. For example the string:
|
1 |
"| |{x}| + Sin[|{theta}| / 2] + 2 Cos[|{theta}| / 2] |" |
Translates into the code:
|
1 |
Ipr.Substitute(@" |{0}| + Sin[|{1}| / 2] + 2 Cos[|{1}| / 2] ", x, theta) |
This is a very useful shorthand for parametric strings generally suitable for scripting purposes.
Note that a square bracket command [: arg |> func :] is first translated into @func( "|arg|" ) so that the argument is actually converted into a parametric text to be later translated into a Ipr.Substitute() method call if needed. In effect we can use a square bracket command with a parametric text argument as in this simple script:
|
1 2 3 4 |
var n = 6; for (var i = 0; i < 6; i++) [: let mv|{i}| = Scalar('|{i}| Pi / |{n}|') |> exec :]; |
After the first step, this will translate into:
|
1 2 3 4 |
var n = 6; for (var i = 0; i < 6; i++) @exec("| let mv|{i}| = Scalar('|{i}| Pi / |{n}|') |"); |
And after the parametric string is translated the script becomes:
|
1 2 3 4 |
var n = 6; for (var i = 0; i < 6; i++) @exec(Ipr.Substitute(@" let mv|{0}| = Scalar('|{0}| Pi / |{1}|') ", i, n)); |
4- Method Shortcuts:
The final step before the script is passed to the CS-Script system is to replace all shortcut names for methods by their correct names. A shortcut is any part of the code on the form @identifier. where An internal dictionary holds all correspondences between shortcut names, which are case insensitive in contrast to C# identifiers, and their actual method names. For example the code:
|
1 |
[: cliff_conj(A|{i}|) |> ev |> as |> apl :]; |
Translates into:
|
1 |
@apl(@as(@ev("| cliff_conj(A|{i}|) |"))); |
Then into:
|
1 |
@apl(@as(@ev(Ipr.Substitute(@" cliff_conj(A|{0}|) ", i)))); |
Then after the final step it becomes:
|
1 |
Ipr.Output.Log.AppendLine(Ipr.AsString(Ipr.Evaluate(Ipr.Substitute(@" cliff_conj(A|{0}|) ", i)))); |
The shortcuts are assigned initially by GMac to the most useful services methods especially implemented by the Ipr member of the generated class. Method shortcuts can be added, changed, and reset using the Ipr.Shortcuts member’s methods. The default shortcuts are presented in the shown table (an html version is here):
As a final example take a look at the following script and compare the translated text after each of the 4 steps:
The Original GMac script written by the user:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//Square wave approximation by geometric operations [:geometry2d.cga |> reset:]; //Initialize GMac multivector variables [: let angle = 't' let unit = Multivector(#e1# = 1) declare signalMv : Multivector |> exec :]; //Construct rotated vectors and add them together to form a multivector signal for (var i = 1; i <= 20; i += 2) [: let signalMv = signalMv + rotate(unit, |{i}| * angle) / |{i}| |> exec :]; //Project multivector signal on vertical axis to get scalar signal. //Then format signal equation using Mathematica var signal = [: signalMv.#e2# |> ValueOf |> AsString |> ComputeToInputForm :]; //Display the symbolic equation of the signal <: signal |> AppendLine :>; //Plot signal between -2 Pi and 2 Pi using Mathematica into a C# image object var img = [: Plot[ |{signal}| , {t, -Pi, 2 Pi}] |> ComputeToImage :]; //Save the C# image object into a file img.Save(@"C:\GMac\fs.bmp"); |
The script after translating square bracket commands:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
//Square wave approximation by geometric operations @reset("|geometry2d.cga |"); //Initialize GMac multivector variables @exec("| let angle = 't' let unit = Multivector(#e1# = 1) declare signalMv : Multivector |"); //Construct rotated vectors and add them together to form a multivector signal for (var i = 1; i <= 20; i += 2) @exec("| let signalMv = signalMv + rotate(unit, |{i}| * angle) / |{i}| |"); //Project multivector signal on vertical axis to get scalar signal. //Then format signal equation using Mathematica var signal = @ComputeToInputForm(@AsString(@ValueOf("| signalMv.#e2# |"))); //Display the symbolic equation of the signal <: signal |> AppendLine :>; //Plot signal between -2 Pi and 2 Pi using Mathematica into a C# image object var img = @ComputeToImage("| Plot[ |{signal}| , {t, -Pi, 2 Pi}] |"); //Save the C# image object into a file img.Save(@"C:\GMac\fs.bmp"); |
The script after translating angle bracket commands:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
//Square wave approximation by geometric operations @reset("|geometry2d.cga |"); //Initialize GMac multivector variables @exec("| let angle = 't' let unit = Multivector(#e1# = 1) declare signalMv : Multivector |"); //Construct rotated vectors and add them together to form a multivector signal for (var i = 1; i <= 20; i += 2) @exec("| let signalMv = signalMv + rotate(unit, |{i}| * angle) / |{i}| |"); //Project multivector signal on vertical axis to get scalar signal. //Then format signal equation using Mathematica var signal = @ComputeToInputForm(@AsString(@ValueOf("| signalMv.#e2# |"))); //Display the symbolic equation of the signal @AppendLine(signal); //Plot signal between -2 Pi and 2 Pi using Mathematica into a C# image object var img = @ComputeToImage("| Plot[ |{signal}| , {t, -Pi, 2 Pi}] |"); //Save the C# image object into a file img.Save(@"C:\GMac\fs.bmp"); |
The script after translating parametric strings:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
//Square wave approximation by geometric operations @reset(@"geometry2d.cga "); //Initialize GMac multivector variables @exec(@" let angle = 't' let unit = Multivector(#e1# = 1) declare signalMv : Multivector "); //Construct rotated vectors and add them together to form a multivector signal for (var i = 1; i <= 20; i += 2) @exec(Ipr.Substitute(@" let signalMv = signalMv + rotate(unit, |{0}| * angle) / |{0}| ", i)); //Project multivector signal on vertical axis to get scalar signal. //Then format signal equation using Mathematica var signal = @ComputeToInputForm(@AsString(@ValueOf(@" signalMv.#e2# "))); //Display the symbolic equation of the signal @AppendLine(signal); //Plot signal between -2 Pi and 2 Pi using Mathematica into a C# image object var img = @ComputeToImage(Ipr.Substitute(@" Plot[ |{0}| , {t, -Pi, 2 Pi}] ", signal)); //Save the C# image object into a file img.Save(@"C:\GMac\fs.bmp"); |
The generated C# class with full code after translating method shortcut names:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
using System; using System.Collections.Generic; using System.Drawing; using System.Linq; using GMac; using GMac.GMacAST; using GMac.GMacAST.Symbols; using GMac.GMacAST.Expressions; using GMac.GMacAST.Commands; using GMac.GMacAPI.Binding; using GMac.GMacScripting; using TextComposerLib; using TextComposerLib.Linear; using Wolfram.NETLink; /// <summary> /// This class represents a GMac script to be executed using an internal script interpreter object /// </summary> public sealed class InteractiveScript : IGMacScript { /// <summary> /// The script interpreter object that executes all script commands /// </summary> public GMacScriptInterpreter Ipr { get; set; } /// <summary> /// The root GMacAST for this script /// </summary> public AstRoot Root { get { return Ipr.Root; } } /// <summary> /// The processing code to be executed /// </summary> public void Process() { //Square wave approximation by geometric operations Ipr.Reset(@"geometry2d.cga "); //Initialize GMac multivector variables Ipr.Execute(@" let angle = 't' let unit = Multivector(#e1# = 1) declare signalMv : Multivector "); //Construct rotated vectors and add them together to form a multivector signal for (var i = 1; i <= 20; i += 2) Ipr.Execute(Ipr.Substitute(@" let signalMv = signalMv + rotate(unit, |{0}| * angle) / |{0}| ", i)); //Project multivector signal on vertical axis to get scalar signal. //Then format signal equation using Mathematica var signal = Ipr.ComputeToInputForm(Ipr.AsString(Ipr.ValueOf(@" signalMv.#e2# "))); //Display the symbolic equation of the signal Ipr.Output.Log.AppendLine(signal); //Plot signal between -2 Pi and 2 Pi using Mathematica into a C# image object var img = Ipr.ComputeToImage(Ipr.Substitute(@" Plot[ |{0}| , {t, -Pi, 2 Pi}] ", signal)); //Save the C# image object into a file img.Save(@"C:\GMac\fs.bmp"); } } |
2.3. The Server: GMacScriptInterpreter Class
After translation of the script into C# code it is passed to the CS-Script system for compilation. If no errors are found a class of type InteractiveScript is added in memory to the GMac system and an instance of the generated class is created and initialized by assigning an existing object of type GMacScriptInterpreter to the Ipr member. The Ipr member is responsible for accessing most scripting services provided by GMac through its public methods. The services provided by this member fall under the following categories:
- Initialization of the GMacDSL Code’s Computational Context: Using the overloaded methods Reset() , OpenScope() , and CloseScope() to set the context in which any following commands will be executed and how symbols are referenced inside script expressions.
- Accessing GMacAST Information: Through the Root member and several methods for accessing GMacAST symbols by their names including the Namespace(), Frame(), BasisVector(), FrameMultivector(), Subspace(), Constant(), Structure(), Macro() , LocalVariable(), Symbol(), and GMacType() methods.
- Compilation, Execution, and Evaluation of GMacDSL Commands and Expressions: Using the ValueAccess(), GMacTypeOf(), ValueAccessExists(), Expression(), Declare(), Assign(), Execute(), ValueOf(), and Evauate() methods.
- Initialize Multivector Values from Patterns and Subspaces: Using the SubspaceToMultivector() methods.
- Low-Level Communication with the Symbolic Engine: GMac uses Mathematica for all its symbolic computations. A set of methods can be used to access the active Mathematica server and execute code directly on its kernel using the ComputeToExpr() , ComputeToString() , ComputeToInputForm() , ComputeToOutputForm() , ComputeToTypeset() , and ComputeToImage() methods.
- Report Values Generated During Script Execution: Through the Substitute(), AsString(), and Output.Store() methods and the Output.Log member (of type LinearComposer explained in the TextComposerLib Guide).
- Create and Update Shortcut Names for Methods: Using the Ipr.ResetShortcuts() , and Ipr.SetShortcuts() methods the user can change, add, or reset the shortcuts associated with methods available for the GMac scripting engine.
2.4. The Manager: GMacScriptManager Class
The GMacScriptManager class is used by the GMacIDE to:
- Translate the script entered by the user into correct C# class definition code, using the GMacScriptGenerator class.
- Compile the generated C# class code in memory using the CS-Script library.
- Execute the compiled code that typically contains many calls to GMac services implemented as public methods by the GMacScriptInterpreter class.
- Report any errors during any of the previous 3 phases to the GMac interface.