Expression Trees Composition
You may have noted that the structured text composers are missing tree structures, one very important data structure in computer science. A simple text tree data structure can be used to compose and manipulate semantic-free expression trees very similar in function to XML markup, but with a more readable text form. The ITextExpression interface, under the TextComposerLib.TextExpression.Ast namespace, is the base of all text expression tree nodes. Two kinds of expressions can be used:
- Simple: The TeLiteralNumber, TeLiteralString, and TeIdentifier classes implement the ISimpleTextExpression interface to represent simple number literals, string literals, and identifiers.
- Composite: The TeList and TeDictionary classes implement the ICompositeTextExpression interface to represent lists of sub-expressions and dictionaries of sub-expressions.
By nesting instances of these classes we can construct arbitrary text expression trees that can be eventually composed, by traversing, into text.
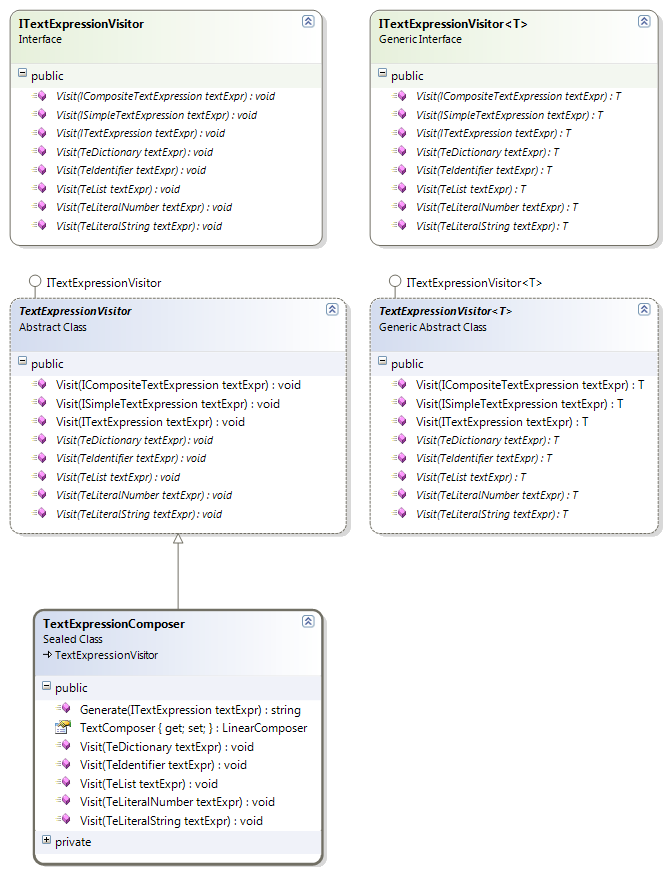
We can use classes that implement from the ITextExpressionVisitor, ITextExpressionVisitor<T> interfaces, found under the TextComposerLib.TextExpression namespace, to implement tree traversing algorithms on the text expression trees. For example the TextExpressionComposer class has the static Generate() method that formats a given text expression tree as a string. Many other tree traversal algorithms can be implemented similarly like search, replacement, or summary creation algorithms.
The shown code can be used to construct a simple expression tree using normal class constructors. This approach is useful when the tree represents information generated internally by the program, and the tree is used to pass the information to other text composition stages for example. The output of this code is as follows:
The second code example parses a given text into a text expression tree using the static ParseToTextExpression() method of the TextExpressionParser static class. Then a custom class called Task1Class derived from TextExpressionVisitor is used to replace the heads of composite sub-expressions in the tree according to a given dictionary.
The definition of the Task1Class is as follows:
The output of this code displays the expression tree before and after the replacement happens:
The syntax of expressions is as follows:
- Number literals can be any familiar integer of floating point number literal like -42 or 2.456e-2 for example.
- String literals can be any C#-like string literal but can also be enclosed by single or double quotes. For example "Me and them", and 'Me and them' are the same string literal.
- An identifier is a sequence of alphanumeric or underscore characters not starting with a number. For example x, Var12, and Rotation_Z are all legal identifiers.
- List expressions optionally start with an identifier called the name of the list and are a comma separated listing of sub-expressions, possibly of mixed kinds, surrounded by square brackets. For example Max[1, 2, 3], Plus[-2.3, 5, 7.9], ["A", "B", 8, R1] are all legal list expressions. There is no specific meaning associated with the lists.
- Dictionary expressions are similar to list expressions but each item gets a key and curly braces are used. For example {X:3, Y:8, Z:-1} and Ray{ Direction : Point[2.3, 7.6], Origin : Vector[3.1, -2.7] } are typical dictionary expressions.
Using this simple Text Expression Tree DSL the user can create arbitrary complex trees of basic numbers, strings, and identifiers. Such trees are similar in structure to the XML trees but much easier to manipulate, process, and store in typical code generation scenarios.